abstract. This Essay examines two alternative designs for hierarchical institutions: “bounded” and “unbounded.” In a bounded structure, a principal decides on a bounded aggregate numerical allocation, and then an agent makes the allocation to an underlying subject population while complying with the bound. In an unbounded structure, the principal provides no aggregate numerical cap, but instead provides some other form of guidance to the agent regarding allocation. An example of a bounded institution is grading to a pre-arranged curve (“X students receive As”), while an example of an unbounded institution is granting a particular grade to each student who meets a particular threshold (“each student who displays mastery of the material receives an A”).

Bounded and unbounded institutions are common in many legal contexts and differ in their strengths and weaknesses. From the principal’s perspective, bounded institutions are increasingly desirable to the extent that (a) there is a homogeneous and large subject population, (b) the agent is likely to be biased or to make systematic errors, and (c) it is difficult to devise other rules to guide the agent’s decision. If agents are biased but otherwise share preferences with the principal—and the principal knows the underlying subject population’s traits—then bounded institutions can produce the precise outcome that the principal wants even though neither the principal nor the agent is fully informed or free of error.

The Essay applies these insights to government appropriations, environmental law, and administrative law (among other areas). Consider, for example, funding scientific research through the National Science Foundation (NSF). Congress should give the NSF a fixed (bounded) budget if it thinks the NSF is biased in favor of funding scientific research and the distribution of quality of scientific research proposals is relatively predictable from year to year. If the NSF always wants to fund the same projects that Congress would, by contrast, then Congress should tell the NSF to fund all research projects the NSF deems worthy, thereby giving the NSF an unbounded source of funding.

author. Professor of Law, Yale Law School. I thank seminar participants at USC Gould School of Law, Brooklyn Law School, and Yale Law School, and the editors of the Yale Law Journal for helpful comments and suggestions. I thank Courtney Dixon for superb research assistance. All errors are my own.

Introduction

To bound or not to bound? While the question is not usually framed this way, policymakers face the choice of whether to “bound” in many legal contexts. Should Congress give government programs a bounded budget (as in discretionary spending) or allow the program budget to be unbounded and spent as needed (as in entitlement spending)? Should Congress bound the Environmental Protection Agency (EPA) by subjecting its regulations to a “regulatory budget,” or should it allow the EPA to enact any regulations that meet a specified standard or rule? Should judges be bound in the total lengths of the sentences they can give, or should criminal sentences be left to judicial discretion? Should governments be required to award a bounded percentage of contracts to minority-owned businesses, or should the government consider minority ownership as a factor in awarding contracts without being bound to any target? Should the National Science Foundation (NSF) have a bounded budget and then award grants to the best projects that conform to the budget, or should the NSF choose a quality threshold and award grants to all projects that meet it—even if there are more or fewer projects meeting the threshold than expected? Should a law school instruct its professors to grade on a bounded curve, or should grading be left to the instructor’s discretion?

In a bounded institutional structure, a policymaking body (the principal) places a binding numerical restriction on one or more dimensions of a subordinate body’s (the agent’s) decision process. The existence of the bound compels the agent to compare subjects who may or may not benefit from a program instituted by the principal but administered by the agent. Budgets, quotas, and curves are prominent examples of bounded institutional structures. In an unbounded structure, by contrast, the agent is not compelled to compare subjects but rather makes separate determinations about each subject.

This Essay has two purposes. The first is descriptive: boundedness is recurrent in law and policy, and there is particular value in naming the phenomenon and applying formal economic tools to explain when and why bounded structures are more (or less) attractive. The second is normative: numerical bounds have many underappreciated practical and theoretical attractions, and they might be used more extensively than they are now.

Before going further, it is important to avoid two possible sources of misunderstanding. First, bounded does not mean “rigid” in the sense of “constrained.” An agent subject to a bound may feel much less constrained than an unbounded agent who must apply precise rules articulated by the principal. Instead of implying rigidity, boundedness refers to the existence of some aggregate numerical requirement that requires direct comparisons of one subject to another. Second, in a world of finite resources, all institutions are bounded to some degree. Entitlement spending, for example, cannot be infinite—even if that is what the programs ostensibly require. But in a bounded institution, the numerical restriction compels comparison among subjects relatively quickly, while in an unbounded structure, the tradeoffs among subjects may become apparent only much later (if they become apparent at all). As a result, I believe the bounded-unbounded distinction will prove fruitful even if it is not absolute.

Bounded and unbounded structures add a new dimension to the voluminous literature on legislative delegation to administrative agencies and other branches. This literature has focused on why legislatures delegate.1 A smaller literature asks to whom legislatures should delegate—agencies, courts, or some other actor.2 Yet another well-developed literature focuses on one aspect of how legislatures should delegate: should the principals provide agents with rules or standards in constraining the agents’ delegated authority?3

The focus on bounded versus unbounded institutional structures introduces a new theme to the literature on how legislatures should delegate to courts and agencies. Bounded institutional structures impose aggregate numerical restrictions on agents and compel agents to make relative determinations among subjects.4 Bounds can coexist with rules, standards, or complete discretion on other dimensions of the agent’s decision-making process. For example, a grading curve specifies the number of each type of grade that the professor can award and compels the professor to compare students to each other. The curve is a bounded institution. But other dimensions of the grading decision may be subject to anything from a strict rule to complete discretion. One educational institution that uses a curve may provide professors with exam questions and grading rules, while another institution that relies on a curve may tell the professors nothing about how to assign grades.

Unbounded institutional structures entail no aggregate numerical cap on the agent’s decision; they allow for anything from strict rules to unspecified discretion regarding that decision. For example, some entitlement spending programs, such as Medicare, obligate the government to “make payments . . . to any person who . . . meets the legal criteria for eligibility.”5 Moreover, the government is not allowed to become involved in medical decision making.6 By contrast, other entitlement programs, such as Social Security, use rules to determine which beneficiaries receive funding and how much each beneficiary receives. Focusing on bounded and unbounded institutional structures allows us to see that, contrary to standard analyses, the question of rules versus standards does not exhaust the question of how principals can (or should) delegate authority to agents.

When principals must delegate and agents are potentially biased, my discussion and model, which build upon the optimal delegation literature in economics,7 offer several recommendations relating to the use of bounded institutions. Bounded institutional structures work well relative to unbounded structures when (1) there is relatively little variation in quality among subjects evaluated by the agent (for example, the quality of scientific grant applications to the NSF does not vary all that much across different applications); (2) agents evaluate a large number of subjects; (3) agents are likely to be biased relative to the principal; and (4) a rule that constrains the agent’s behavior is impractical (for example, scientific quality is difficult to specify by rule, and a rule that attempted to do so would lead to poor funding choices).

Unbounded institutions, by contrast, outperform bounded institutions when subject populations are small and inconsistent. Bounded budgets for government departments subject to idiosyncratic needs—such as the Federal Emergency Management Administration (FEMA)—are a bad idea. Instead, FEMA and similar departments are better off with more flexible unbounded budgets that can respond to unexpected needs (such as those created by a catastrophic hurricane). In addition, unbounded institutions perform better when agents share preferences with the principal. For example, if the NSF demonstrates expertise in evaluating grant applications and shares Congress’s preferences over how many projects to fund, then it should be trusted with an unbounded budget. The unbounded budget would allow the NSF to respond when the number of worthwhile applications is unusually high or low.

In some circumstances, the optimal delegation literature demonstrates that bounded institutional structures can approximate ideal outcomes even though neither the principal nor the agent is fully informed or free of bias.8 Suppose, for example, that Congress is incapable of evaluating specific scientific proposals but has a general sense of how many scientific research projects are worth pursuing each year.9 Further suppose there are a large number of independent grant proposals submitted to the NSF each year, but the NSF is biased and values science more than Congress does. Left to its own devices with an unbounded budget, the NSF would fund more projects than Congress would like. But assume the NSF is good at judging proposals in relative terms, and the NSF’s comparative evaluation of proposals would be the same as Congress’s. Under these assumptions, Congress should pick a bounded budget for the NSF that reflects Congress’s general understanding of the public benefits of science. It should then order the NSF to allocate that budget according to the NSF’s discretion. This bounded institution allows the right projects to receive funding—because the NSF is a good evaluator—but prevents the NSF’s pro-science bias from producing more projects than Congress wants. The fact that bounded institutions can produce ideal outcomes in relatively unpromising situations (with inexpert principals and biased agents) demonstrates that bounded institutions are a promising institutional structure in many cases.

The Essay is organized as follows. Part I provides more detail on the distinction between bounded and unbounded institutions. Part II examines the strengths and weaknesses of each type of institutional structure under different conditions. Part III applies the insights of Part II to EPA regulation, government spending policy, the use of quotas to prevent racial or gender bias, and judicial sentencing disparities. Part IV concludes by arguing that the virtues of bounded institutions may be underappreciated and that bounded institutions themselves may be underused. The Appendix to the print and PDF versions of this Essay explores a formal economic model of bounded and unbounded institutions, and derives the results described in Part II.

I. bounded and unbounded institutions

Let me offer a brief word on how the argument will proceed: I typically begin with an abstract and formal description of the “problem” and then provide more concrete examples to illustrate the abstract principles.

A. Defining Bounded and Unbounded Institutions

1. Principals, Agents, and Bounded Institutions

This Essay examines hierarchical institutions in which a superior body (the principal) sets policy and a subordinate body (the agent) implements (or allocates) that policy.10 The policy choices are made with reference to subjects, who are affected by both the principal’s and the agent’s decisions. The subjects differ in quality (for example, academic achievement in the grades context). The principal wants allocations to be a function of subject quality. For example, students who demonstrate better achievement should get better grades. The quality of the subjects is observed by the agent, but cannot be verified by the principal.

With respect to funding for scientific research, Congress (the principal) wants to fund scientific research (the policy) and assigns implementation of this policy to the NSF (the agent). The subjects of the NSF’s decisions are scientific research grant proposals, which differ in quality—roughly defined as the prospective gain in knowledge per dollar associated with each proposal. Congress wants to fund the highest-quality grant proposals. The NSF observes the prospective gain in knowledge per dollar associated with each proposal, but Congress cannot verify this information. Congress may lack the expertise to understand scientific quality, or scientific quality may have so many dimensions that it cannot be easily verified by anyone besides the agent.

The principal knows the distribution of subject quality within the population11 but cannot determine any individual subject’s quality. Instead, the principal relies on one or more agents to observe and determine subjects’ quality and allocate benefits accordingly.12 However, in observing subject quality, an agent may have some “bias” relative to the principal. Bias means that the agent systematically perceives subjects as having higher or lower quality than the principal would perceive, were the principal able to observe subject quality directly.13

In the scientific research funding context, Congress has a sense, from prior years of funding scientific research, of the quality of the typical grant proposal, as well as how the quality differs from proposal to proposal. But Congress is unable to evaluate the quality of individual scientific proposals. Instead, Congress must rely on the NSF, an agency with expertise in judging the merits of these projects. The NSF’s expertise enables it to make an informed judgment about each grant proposal’s quality. The NSF shares Congress’s goal of funding the research proposals that will produce the most knowledge per dollar.14 But the NSF may not share Congress’s opinion about the quality of any given proposal. For example, if the NSF thinks the benefits of science are greater than Congress does (or if the NSF thinks the costs of funding are lower than Congress believes), then the NSF is “biased” in its evaluation of grant proposals.

After observing subjects’ quality, the agent determines the policy allocation. The principal may choose to impose or refrain from imposing a bound on the agent’s allocation decisions. A bound is a numerical limitation on some dimension of the agent’s policy allocation to subjects. When the principal imposes a bound, the agent allocates X to the subjects based on the agent’s observation of the subjects’ quality and the bound’s restriction; this process requires comparing subjects.15 If there is no bound, then the agent allocates to the subjects based on the agent’s observations, but the agent is not compelled to compare subjects directly to one another.

With respect to the NSF, the “policy allocation” consists of the foundation’s grant-making decisions. To make funding decisions, the NSF uses its observation of each grant application’s scientific merit. If the NSF has no explicit budget, then it chooses to fund all scientific projects that it believes are worth funding. Congress subsequently provides the money for all grant applications approved by the NSF. Alternatively, Congress could provide the NSF with a limited budget for funding grant applications.16 If Congress imposes a bounded budget, then the NSF must stick to that budget; it will fund the highest-quality grant applications until the budget is filled. The bounded budget compels the NSF to compare the quality of one proposal directly to that of another, rather than comparing the quality of each proposal to an absolute standard. If the NSF (when subject to a budget) refuses to compare quality across applications, then it violates its (and Congress’s) goal of providing the most knowledge per dollar.

The principal dislikes errors. An error occurs when a subject is allocated more or less than the principal thinks the subject should be allocated. To avoid such errors, the principal decides whether to constrain the agent’s decision process by imposing a bound, which can reduce allocation errors.

In the context of scientific funding, an error occurs when a grant proposal that has a desirable “knowledge per dollar” value (from Congress’s perspective) fails to get funding, or when a grant proposal that has negative knowledge per dollar value (from Congress’s perspective) is awarded funding. Congress will bound the NSF’s research budget if it expects less costly funding errors with a bounded NSF budget than with an unbounded one.

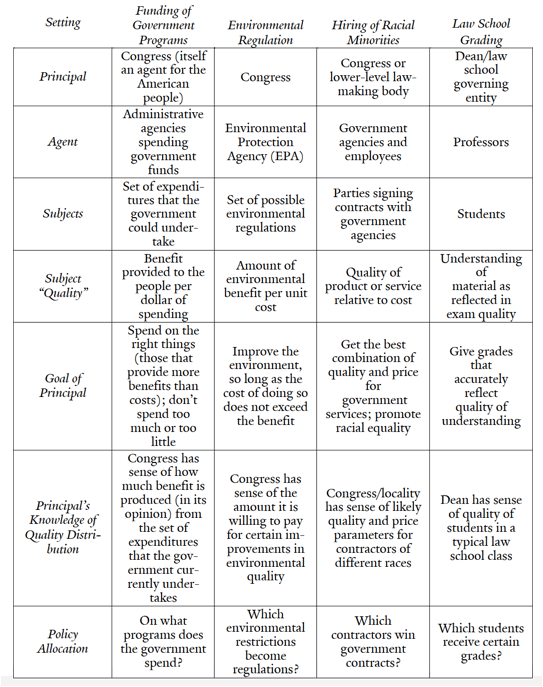
Table 1 provides a sketch of how this abstract framework applies in non-NSF contexts.

Table 1.

applications of bounded and unbounded institutional structures

2. Simplifying Assumptions

To make the analysis tractable, I make several unrealistic assumptions that allow me to focus on the tradeoffs between bounded and unbounded institutions. I do not mean to imply that the considerations addressed below are unimportant. Instead, I leave their analysis to other papers, past and future.

a. Two-Tiered Institutions

This Essay focuses on two-tiered institutions with a policymaking principal and an implementing agent who makes decisions about subjects based on the agent’s perception of the subjects’ quality. In reality, hierarchical institutions have multiple tiers.17 The choice between bounded and unbounded institutions explored here therefore exists at many levels. In a three-tiered institution, the top-level body may set an unbounded standard for the second-level body, while the second-level body may impose a bounded constraint on the third tier. The top level may also insist that a bounded constraint be applied to the third tier. In each case, the costs and benefits discussed here should govern the choice between unbounded and bounded institutions at any level of a hierarchy.18

To illustrate this point: when I examine the relationship between Congress and the NSF, I assume that Congress is a single agent with well-defined preferences, ignoring the fact that Congress is an agent for the American people and that Congress may not have well-defined preferences. I also assume that the NSF is a single agent or group of agents, ignoring the NSF’s internal hierarchy.

b. Sharing of Relative Quality Perceptions

While the agent may be biased—in the sense that the agent and principal have different perceptions of subject quality—I assume that the principal and the agent’s quality determinations are related in an important way. If the agent were asked to rank the subjects by quality, the agent would give the same “relative” ranking as the principal. In other words, the agent may be biased in the sense of having a higher or lower observation of the subjects’ absolute quality. But, if asked to make relative determinations, then the agent and the principal would produce the same rank ordering and identify the same quality “distance” between subjects.19

To illustrate the relative quality assumption in the context of grading, a professor may give a student an 80 out of 100 while the dean would assign a 90 out of 100, but if the professor were to grade the students in a class, the professor’s grades for each student on a scale of 100 would always be ten points lower than the dean’s. The professor’s grading tendencies can be “generous” (grades are systematically too high) or “stingy” (grades are systematically too low), but the relative quality assumption means that the dean and professor share a rank ordering of the students, as well as an identical sense of how far one student’s performance is from another’s. In the context of funding for scientific research, the NSF may have a consistently higher or lower opinion of the benefits of scientific research than Congress does, but the NSF agrees with Congress on which projects are more meritorious than others, and by how much.

By assuming that principals and agents share rank-order assessments of quality, I assume that the agent’s observations provide valuable information to the principal about the subject, even if the principal does not necessarily agree with the agent’s judgments. By contrast, if there is no relationship between the principal’s and agent’s rank-order assessments, then the principal may not want to rely on the agent to perform any allocation, since the agent’s allocation will share nothing with the principal’s. (In this case, the principal may as well allocate to subjects at random and save the cost of paying for the agent.)

c. No Strategic Behavior

I assume that the introduction of a bounded or unbounded restriction on agent behavior does not change the behavior of the subjects.20 Therefore, a curve does not cause students to work harder even though they are competing against their classmates. While such strategic behavior is undoubtedly present, it is the subject of a long literature.21 In order to focus on the role of principal/agent problems in the choice between bounded and unbounded institutions, I assume that these undoubtedly important interactions do not play a role.

d. Random Assignment of Subjects to Agents

In cases in which the principal relies on many agents to evaluate subjects, I assume that each agent gets a random sample of the subject population to evaluate. This assumption excludes, for example, the possibility that students of low quality choose professors who are known to be easy graders. This assumption means that the analysis developed below is most applicable to situations such as assigned classes.

e. Optimal Agent Response to Bounds

I assume that when the bound constrains the agent, the agent responds in a way that is best for the agent. For example, suppose that the NSF, left to its own devices, would like to award $2 billion in funding for research but that Congress has only appropriated $1 billion. In response, the NSF will choose to fund the $1 billion in projects that it thinks will produce the most valuable scientific knowledge. This assumption means that the agent does not change its preferences because of the bounds. For example, the NSF does not fund poorly conceived projects instead of well-conceived projects because it is angry about its limited budget.

f. Principal Knows the Distribution of Subject Quality

Unless stated otherwise, I assume that the principal knows the distribution of subject quality even though the principal cannot observe the quality of any specific subject. This assumption means that even though the principal cannot get involved in determining any subject’s quality, the principal has a sense of the average subject quality and the variability of quality across subjects. In the NSF context, Congress knows the average quality, and the variability of the quality, of the scientific research grant applications that the NSF receives.

B. The Scope of Bounded and Unbounded Institutional Structures

1. Bounded Institutional Structures and Rules and Standards

With bounded and unbounded institutions defined, we can now precisely describe the difference between bounds and rules. When using rules, principals specify ex ante how agents should allocate to subjects based on “factual” characteristics.22 While the principal would ideally like to specify rules based on quality, quality is unobservable to the principal.23 Instead, the principal specifies the agent’s action as a function of some other characteristic that is observable, verifiable, and imperfectly correlated with subject quality.

A rule prescribes the agent’s action as a function of a characteristic of the subject’s quality. The rule does not ordinarily prescribe the agent’s action with respect to one subject as a function of the characteristic of another subject. Consider speed limits, a paradigmatic example of a rule.24 Driving speed is a characteristic that is correlated with “driving quality,” measured by the risk of harm to others that results from one’s driving. With a speed limit, a principal tells police officers how to allocate speeding tickets as a function of a subject’s driving speed. With a speed limit rule, the driving speed or riskiness of other drivers is not relevant. If the driver goes over the prescribed speed, then the rule specifies that the driver should be sanctioned, regardless of the behavior of other drivers. With a bound, by contrast, the principal specifies an aggregate limit that is not explicitly a function of any characteristic. Because the bound is an aggregate numerical limit that applies to all of the agent’s actions, the bound requires the agent to compare subjects to each other. After all, the allocation an agent makes to one subject has an effect on what is available to allocate to the other subjects. This would not be the case with a rule.25

Bounds and rules are similar in the sense that both are solutions to the problem of how a principal should optimally delegate to an agent. In addition, one of the primary costs of both bounds and rules is a reduction in agent flexibility. But these similarities should not obscure the core idea that bounds and rules constitute two different solutions to the problem of optimal delegation.

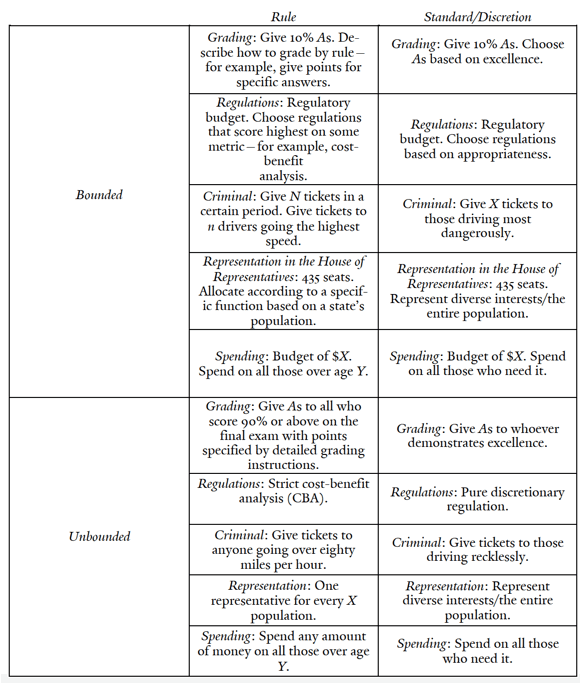
Not surprisingly, a bound can coexist with a rule, a standard, or complete agent discretion. An unbounded structure can also coexist with a rule. To illustrate the relationship between bounded and unbounded institutional structures and the conventional divide between rules and standards, Table 2 presents a matrix.26

Table 2 demonstrates that principals can bind agents to limit an allocation while still allowing agents considerable discretion along other dimensions. Grading according to a curve provides a familiar example: while many schools specify grading curves, they seldom specify how the professor should grade an exam. Instead, the professor is free to grade as desired, so long as the distribution of grades adheres to the curve. The principal dictates the distribution of grades but gives little or no guidance on how to assign them.

Numerical bounds also can be combined with rules.27 The House of Representatives has 435 seats, and these seats are apportioned to states based on population.28 In this case, the principal provides a bound on the total number of seats in the House of Representatives (435) and a rule regarding how to allocate them (states with higher populations get more representatives according to a formula).29 If Congress decided to increase or decrease the number of representatives, then the allocation rule could easily be altered accordingly.

Unbounded institutions can also be combined with rules or discretion. In the speeding example, an unbounded rule might say, “Give tickets to any driver going over eighty miles per hour.” The number of tickets issued by the agent (“how many”) is determined by the number of drivers violating the eighty mile per hour rule. An unbounded discretionary standard, by contrast, exists when the agent faces no clear rule for determining either “how many” or “to whom.” If the principal tells the subordinate to “give tickets to those driving recklessly,” then this is an unbounded standard.

2. Does the Typical Institution Have a Bounded or Unbounded Structure?

The default institutional structure is both bounded and unbounded. If the principal does not impose a numerical limit on the agent’s behavior, then the agent is formally unbounded. Nonetheless, any resource constraint on an agent functions as a bound. If the agent cannot simply increase his or her resources unilaterally, then the agent’s allocation is limited by this resource limitation. For example, an administrative agency cannot promulgate an infinite number of rules if it has limited resources. Nevertheless, this implicit resource constraint presents a very different limitation on agent behavior than a more specific bound. An agency with few resources and unbounded rulemaking authority may make very different rules than an agency with greater resources and strict bounds (such as a regulatory budget) on its rulemaking authority.

As the preceding paragraph indicates, hybrid unbounded/bounded institutions can exist. Lower-level bodies can face bounded constraints along some dimensions and unbounded constraints along others. In addition, lower-level bodies can face directions that combine elements of bounded and unbounded instructions along the same dimension. Again, grading proves illustrative. Grading curves are often not precisely bounded. Instead of prescribing an irreversible number or percentage for each grade, curves often prescribe a range. At the top of the curve, for example, professors may be allowed to give 2% to 5% of the class a grade of A+. Within this narrow range, the professor’s ability to award an A+ is unbounded. Another possibility is an asymmetric bound; the professor can award an A+ to no more than 5% of the class, but the professor can give as few as zero A+ grades. Hybrid institutions such as the grading systems described here will have some of the costs and benefits of both bounded and unbounded institutions. For simplicity, however, this Essay focuses on the extremes—numerically bounded and unbounded institutions.

Table 2.

rules, standards, bounded and unbounded institutions

 II. bounded versus unbounded institutional structures

With the principal’s choice between bounded and unbounded institutional structures now defined, this Part analyzes circumstances favoring the use of one structure over the other. Under some conditions, bounds increase error costs, making them undesirable for the principal. Under other conditions, bounds decrease the cost of policy allocation errors. In the Appendix to the print and PDF versions of this Essay, I present an economic model that derives many of the results that I describe here.

A. Unbiased Agents

Assume, for purposes of this section, that the agent receives a perfect signal about the subjects’ quality. In addition, the agent is unbiased. (By which I mean, again, that the agent shares the principal’s rank-order preferences regarding allocation.)

Under these circumstances, unbounded institutional structures are preferable to bounded structures.30 Unbounded institutional structures always produce the principal’s preferred outcome because the agent observes each subject and shares the principal’s preferences. As a result, the agent produces the allocation that the principal would have produced if the principal could observe each subject’s quality. There is no reason to constrain such an agent with a bound.

By contrast, under these same conditions, bounded institutional structures make errors inevitable. Instead of allowing the unbiased agent to make choices that would be identical to the principal’s, the bound constrains the agent to make different choices.

The superiority of unbounded institutions in the context of unbiased agents can be illustrated using environmental protection regulations. Suppose the EPA chooses regulations exactly as Congress would want it to. In this case, a regulatory budget is harmful. Without a regulatory budget, the EPA chooses Congress’s preferred regulations. With a budget, by contrast, some regulations may be precluded. In any year, there may be more or fewer efficient and new environmental regulations than there would be in a typical year. However, the problems of a bounded curve are reduced when the population of possible regulations is stable, because the chance that a year will have an atypically strong or weak set of regulations is lower.

B. Biased Agents

Now assume that the agent makes biased determinations of subject quality. In other words, the agent systematically overestimates or underestimates the desirability of a particular allocation relative to the principal.

1. Benefits and Costs of Bounded and Unbounded Institutional Structures

a. Theory

For bounded structures, the principal chooses the budget for a particular agent based on the true population mean and the number of subjects that are evaluated by the agent. Because of the bound, the agent no longer chooses allocations for each subject based solely on the agent’s bias.31 Instead, the agent chooses allocations based on the relative quality of each subject and the bound that the agent must meet with respect to all subjects. Therefore, a bound adjusts for bias: an agent who is downwardly biased in determining quality relative to the principal will be forced to raise her allocation as a function of quality while an agent who is upwardly biased will be compelled to lower her average quality allocation. Establishing the bound, however, introduces some of the costs described in the previous Part. The agent must comply with the bound—and if the bound is poorly chosen for the group of subjects, then the allocation chosen by the agent may be bad for the principal. For example, the sample of subjects that comes before the agent may differ from the population distribution. In this case, the bound may require over- or under-allocation, regardless of the agent’s bias.

If the principal knows that the agent is biased in a particular direction, then unidirectional bounds may be appropriate. For example, if the agent is likely to be upwardly biased, then a cap (without a floor) becomes desirable for the principal. The cap constrains the agent’s upward bias, while the lack of a floor means that, if subject quality happens to be unusually weak, then the agent can allocate accordingly.

b. Application to the National Science Foundation

Consider Congress’s choice of whether to impose a grant-making budget on the NSF (the current practice) or to allow the NSF to fund all projects that the NSF thinks are worth funding. Suppose further that the NSF is biased: it places a higher value on scientific research than Congress does. If Congress chooses a bounded institutional structure for the NSF, it budgets a certain amount for funding research and then charges the NSF with allocating those funds to different grant applications (subjects). If Congress chooses an unbounded structure for the NSF, then it allows the NSF to provide grants to any scientific projects that the NSF deems worthy.

Both bounded and unbounded structures offer advantages and disadvantages to Congress. If Congress imposes a bounded grant-making budget on the NSF, then the misallocation caused by the NSF diminishes (or is even eliminated). The grant-making budget prevents the NSF from indulging its pro-science bias and forces the NSF to make funding decisions based on the budget and the relative merits of the grant applications forwarded by scientists. On the other hand, if the grant applications that come before the NSF prove to be systematically better or worse than Congress expected when it formulated the budget, then requiring the NSF to stick to the budget may result in funding too few or too many grant applications (from Congress’s perspective).

If Congress allows the NSF to provide whatever funding the NSF deems appropriate, then the NSF can indulge its pro-science bias. The NSF will fund more grant applications than Congress would like. Without a budget, funding one project does not reduce funding for any other projects. Although Congress loses control over NSF bias if it uses an unbounded funding structure, it gains flexibility. If the quality of grant applications is much higher than Congress expected, the unbounded NSF can respond instantly and fund more projects.

When choosing between a bounded (discretionary) budget allocation for the NSF and an unbounded (entitlement) budget structure, Congress should weigh the benefits and costs of each institutional structure.

2. Factors Favoring the Choice of a Bounded Institutional Structure

a. Theory

The principal should choose a bound when the benefits of bias correction exceed the costs of rigidity and potential misallocation. The bound is most attractive to the principal when the agent’s bias is high,32 the variability of quality within the population is low,33 and the agent faces a large sample of subjects.34 These factors either increase the benefits of bias reduction or decrease the costs of the rigidity imposed by a bound.

As the number of subjects gets very large, a bounded institutional structure produces a perfect allocation in spite of the agent’s bias.35 With a large number of subjects, the distribution of quality within the agent’s sample population becomes indistinguishable from the total population distribution. When the bound accurately captures the distribution of the subjects—and we are assuming that the principal has perfect knowledge of the distribution of quality in the population—the rigidity costs of the bound become negligible. The bound’s bias correction benefits remain robust as the number of subjects gets larger, since the agent’s bias does not decline as the number of subjects increases; indeed, the bound eliminates the misallocation associated with bias. Moreover, because bias is the only source of agent error—recall that the agent would rank subjects the same way as the principal—the bound produces the best allocation from the principal’s perspective.

b. Application to the National Science Foundation

A bounded budget produces rigidity that the NSF cannot undo. The NSF’s funding for science must be equal to the appropriated amount. This rigidity is good for reducing the impact of NSF bias, but the rigidity is bad for responding to unexpected shifts in the quality of science research from year to year.

When the NSF is highly biased—its “pro-science” leanings relative to Congress are significant—then a budget becomes more attractive. Left to its own devices, a highly biased NSF will fund much more scientific research than Congress would prefer. A budget prevents such overfunding.

When the quality of scientific grant applications is highly variable, a bounded NSF budget becomes less attractive to Congress. High variation in quality from grant application to grant application makes Congress’s budget riskier. If there happens to be a year in which the quality of projects is surprisingly low, then forcing the NSF to fund a budgeted amount of research leads to overfunding. In contrast, allowing the NSF to choose funding based on its own perceptions of each project permits funding for scientific research to adjust to the highly variable nature of scientific inquiry. Note that different areas of scientific inquiry may have different degrees of variation in quality. As a result, Congress may want to impose budgets for some areas of research (where Congress can be confident about quality), but not impose budgets for subjects of research that experience more fluctuation in quality from year to year.

When there are many grant applications to the NSF each year, imposing a budget on the NSF becomes more attractive to Congress. To see this, compare particle physics research with biological research. Particle physics research often requires spectacularly expensive equipment.36 As a result, there are relatively few applications for funding for particle physics research equipment. Instead, scientific organizations make occasional decisions about whether to fund multi-billion dollar projects. In these circumstances, a budget for particle physics research makes little sense. A particle accelerator should either be built or not built, and Congress cannot rely on competition for funding among particle physicists to constrain the NSF.

In biology, by contrast, research apparatuses are often much less expensive.37 Instead of relying on one primary accelerator, biological research advances in hundreds or thousands of labs throughout the country, each of which can make independent requests for equipment. As a result, a budget for research in biology is more attractive than a fixed budget for particle physics. With a fixed budget for thousands of applications, Congress can force the NSF to make direct comparisons among many “desirable” subjects that the NSF, if left to its own devices, would have preferred to fund. This constrains the NSF’s possible pro-science bias. Relatedly, the availability of many different projects makes the typical quality of the proposals easier for Congress to predict, as the law of large numbers applies more precisely to a larger sample.38

3. Perfect Outcomes with Imperfect Principals and Agents

a. Theory

With many subjects, a bound produces the principal’s ideal allocation of resources to subjects even if the principal does not know the size or direction of the agent’s bias.39 With many subjects, the rigidity imposed by a bound becomes less costly. The law of large numbers means that the quality of the subjects “evens out,” enabling the principal to make a very good prediction about the right amount of funding. With a good prediction, a budget produces less rigidity.

While the rigidity problem of a bounded budget becomes insignificant as the number of subjects grows very large, the bias-reducing benefits of a bounded budget do not decrease with the number of subjects. As long as the principal and agent share a rank ordering, the bound compels the agent to adjust the allocation in proportion to the size of the agent’s bias.

With many subjects, a bounded institutional structure thus leverages the information associated with many different observations to minimize rigidity while eliminating bias. As a result, bounded structures can obtain perfect outcomes for the principal.

b. Application to the National Science Foundation

When Congress knows the average quality of scientific projects—and when there are many such projects—Congress can use a budget to get its ideal amount of funding for science, even if the NSF is biased in favor of science funding. Why do we get the right amount of science funding even though the NSF is biased in favor of science and Congress is incapable of judging individual scientific proposals? With many scientific proposals, Congress can be confident that it knows the average quality of the proposals, even if it cannot judge the quality of any particular proposal. Consequently, Congress will produce a budget that gets the total amount of funding correct. The budget constrains the NSF: instead of funding all the projects that it wants to, the NSF has to confine funding to the amount that Congress determines. Therefore, the NSF’s bias cannot be expressed in policy. But because the NSF is still a good judge of relative merit, it will allocate its budget to the scientific projects that Congress would have picked had Congress been able to judge merit.

C. Error-Prone Agents Without Bias

1. Theory

Instead of being systematically biased relative to the principal, an agent may make mistakes of another kind: the agent wants to implement the principal’s wishes—without bias—but makes mistakes. In other words, the agent is a “noisy” but unbiased representative of the principal’s wishes.

I focus on systematic mistakes—mistakes that the agent repeats with all subjects. From an ex ante perspective, the agent is not biased: the agent’s average mistake relative to the principal’s wishes is zero. Sometimes the agent errs by being too optimistic about subject quality; at other times the agent is too pessimistic about quality. On average, the agent is neither consistently optimistic nor consistently pessimistic. But from an ex post perspective, unbiased agents making systematic mistakes appear much like biased agents. They make the same mistake with respect to each subject, just as a biased agent does. In the next period, the agent may make the opposite mistake, but in this period the agent is consistently optimistic or pessimistic relative to the principal.

Principals should prefer bounded structures relative to unbounded structures when agents make large systematic errors. The larger the agent’s systematic error, the more the agent’s final allocation will deviate from the principal’s ideal. Because bounded structures limit the scope for agent deviation, they are relatively more appealing when the agent’s deviations are large.

Principals should also prefer bounded structures when agents make systematic errors and the quality of subject populations does not vary widely. With less quality variation, the rigidity introduced by the bound imposes fewer costs because the budget instituted by the principal is more likely to be accurate.

For similar reasons, principals should prefer bounded structures when error-prone agents allocate to more subjects. With more subjects, the law of large numbers means that the bound is more likely to be accurate and that there are lower rigidity costs associated with the bound.

Thus, with a sufficiently large number of subjects for each error-prone agent, a bounded structure achieves an ideal outcome for the principal. As the number of subjects gets large enough, a budget becomes increasingly accurate as variation from subject to subject “averages out.” Consequently, the bound’s rigidity costs grow small, while the bound’s benefits in terms of reducing the costs of the agent’s repeated errors remain constant. As a result, a bounded budget produces an outcome approaching perfection (from the principal’s perspective).

2. Application to the National Science Foundation

Suppose that the NSF is not biased in favor of science relative to Congress. Instead, the NSF makes mistakes. In some years, the NSF consistently overestimates the quality of grant applications, while in other years the NSF consistently underestimates the quality of grant applications. This situation might arise if the NSF aims to be a truthful agent of Congress but is subject to “fads” in science. Sometimes the fad is to be overoptimistic about the utility of a line of inquiry in science; other times the fad unnecessarily denigrates the quality of a line of research.40

By using a budget for certain areas of science, rather than allowing the NSF to fund whatever the NSF thinks worthwhile, Congress can reduce the impact of scientific fads. The budget ensures that a faddish area does not receive excess funding in spite of the NSF’s attraction to the fad. Conversely, a budget for “areas of science” ensures that research in unpopular areas is not punished simply because it is “out of fashion” from the viewpoint of an NSF that lacks the appropriate perspective.

Congress should therefore be more inclined to give the NSF a budget for particular fields of science when there are more grant applications per area, when the NSF is more subject to fads, and when a particular scientific field experiences less variation in grant application quality.

D. Principals with Imperfect Population Information and Agents with Different Preferences

The previous sections assumed that the principal possessed perfect information about the distribution of quality within the population. There was risk—the principal did not know the quality of any particular subject or group of subjects—but there was no uncertainty: the principal knew the distribution of quality. This assumption is unrealistic. Not only is the principal typically unable to observe any individual subject’s traits, but the principal is also unlikely to know precisely what the average value of quality is, or how quality varies from subject to subject within the population.

More generally, when the principal has more uncertainty regarding the distribution of quality within the population, bounded institutions become less attractive relative to unbounded institutions. Consider an extreme case in which the principal has no information regarding the distribution of quality but the principal still wants to allocate according to quality. In this case, a bounded institution can only do harm. The principal has no information upon which to base the bound; any bound restricts the agent, who has relevant information about quality, without necessarily reducing the agent’s error. As a result, the principal should choose an unbounded institutional structure.

More realistically, the principal possesses imperfect information about the distribution of quality in the subject population. All other things equal, the principal should prefer unbounded institutions when there is greater uncertainty about the population distribution.

When the population is stable, the principal is more likely to obtain accurate knowledge regarding the distribution of quality. Suppose, for example, that the principal learns something about the population distribution each year. When the population is stable, then, over time, the principal acquires highly accurate information. However, when the population is in flux (or, more precisely, when the population is in flux in an unpredictable way), then the predictive value of the principal’s previously acquired knowledge is reduced. With poorer quality information about the population distribution, the principal should be less inclined to impose the rigidities of a bound upon agents.

To be more concrete, suppose Congress does not know the average quality of grant applications. In this case, an NSF grant-making budget becomes less attractive. The effectiveness of the budget depends heavily on Congress’s knowledge of the quality distribution of research applications and the predictability of those applications. If the distribution is unknown, then imposing a grant-making budget becomes less attractive because the budget itself cannot be tethered to the typical quality of grant applications. The more Congress feels it has a sense of the distribution of the quality of grant applications, the more Congress should rely on a bounded budget as opposed to an unbounded structure.

What if the agent’s perception of variation in subject quality differs from the principal’s? Suppose, for example, that the biased agent and principal share the same rank ordering of subject quality but the principal and agent disagree about the difference in quality between two subjects. For instance, the principal thinks subject quality is tightly bunched, while the agent perceives greater differences between subjects. Under these circumstances, a principal who knows the true distribution of subject quality can impose a stricter bound upon the agent. Not only should the principal compel the agent to award a bounded “average” allocation, but the principal should also restrict the variance of the allocation. Agents would be required to submit an allocation with a specified mean and a specified variance, thereby forcing the agent to allow for variance in the subject population that accords with the principal’s perceptions. In this way, the principal can compel the agent to allocate in a more “bunched” manner than the agent would on his or her own.

To be effective, this solution requires that the principal have very good information about the population (both its average quality and the dispersion of that quality), as well as a large number of subjects (to ensure that the dispersion of quality in the sample is similar to the dispersion of quality in the population). With smaller sample sizes or imperfect information about the distribution of quality in the population, the principal should be more reluctant to impose a bound, and especially reluctant to impose a bound that restricts not only the average allocation, but also the dispersion of that allocation.

To be concrete, suppose that Congress thinks that the quality of most scientific grant applications is “bunched.” The NSF, by contrast, has a higher opinion of the average quality of scientific grant applications but thinks that grant applications are more dispersed in quality. In this case, Congress should fix the NSF’s funding budget and tell the NSF to spread that budget more widely than it otherwise would. If Congress has no idea about bunching, or does not think there are enough applications for bunching to recur year after year, then Congress should be more inclined to impose a simpler budget without providing any advice to the NSF about how it should disperse that fixed budget.

Finally, can we say anything about the value of bounded institutions with agents who are worse than biased? For example, the agent’s opinion about the subject’s quality may be uncorrelated with the principal’s. In this case, neither bounded nor unbounded institutions offer much to the principal. Instead, the principal should avoid delegation to such a “maverick” agent.

E. Rules Versus Bounds

The model developed in this Part can also be applied to the choice of rules as opposed to bounds. A rule specifies agent action as a function of some observable characteristic of the subject. Unlike a bound, a rule does not mandate that the allocation to one subject depend upon the allocation to other subjects. Without more, rules merely generate an unbounded institutional structure in which agents are required to follow the rule.

The desirability of rules relative to bounds (or unbounded structures with standards or discretion) depends upon the availability of a good proxy for subject quality. If subject quality is observable and verifiable, and therefore can be used as the basis for a rule, then rules are superior to both bounded and unbounded structures. When quality is observable and verifiable, the principal can obtain the best outcome by specifying precisely what the agent is to do with a subject of any quality.

If there is no good proxy for subject quality that can be used as the basis for a rule, then rules become less attractive. When the principal instructs the agent to behave according to a rule that is a function of some subject characteristic that is only slightly correlated with quality, then the principal experiences a loss each time the agent executes the rule. The size of the loss depends upon the difference between the proxy and the underlying quality that is the principal’s true interest. If there are no characteristics that are proxies for subject quality, then the only rule available to the principal is to command that the agent allocate the same amount to each subject. This outcome is likely to be very costly to the principal.

In choosing between rules and bounds, the principal should prefer bounds under the following conditions, other things being equal:41

1.          Poor observable and verifiable proxies for subject quality. As indicated in the previous paragraph, as the correlation between a proxy for subject quality and true subject quality grows weaker, the performance of a rule that is a function of the proxy deteriorates. Bounds, which specify agent actions in the aggregate but do not specify allocations to a particular subject, become more attractive to the principal when the principal cannot effectively prescribe what to do with each subject.

2.          Less quality variation from subject to subject and more subjects per agent. As described in Part II.B, bounds function better under these circumstances. When bounds perform well, the principal prefers them to imperfect rules, all else being equal.

In the absence of a perfect proxy for subject quality, bounds should be preferred to rules as the number of subjects per agent grows large. As shown in Part II.C, bounds approximate the ideal outcome when the number of subjects grows large. Imperfect rules, by contrast, do not become less imperfect when they are applied to more subjects. As a result, bounds outperform rules as the number of subjects grows large.

This Part has examined the relative performance of bounded and unbounded institutional structures under many different conditions. The next Part applies these lessons to enrich a number of discussions concerning the way in which legislatures should delegate to agencies and courts.

III. bounded versus unbounded structures in action

Bounded institutional structures are common but far from omnipresent. For example, government spending is subject to monetary budgets in many important instances, but Congress chooses unbounded entitlement-like spending in many other cases. This Part applies the analysis of bounded institutions to a number of pressing problems of institutional design and makes normative suggestions regarding the appropriate use of bounds.

A. Traditional Regulatory Oversight Versus Regulatory Budgeting

The analytical framework just developed applies to the problem of controlling administrative agencies. Administrative agencies can be thought of as agents of a principal—perhaps Congress, the President, or the American people. Agencies evaluate a “population” of potential regulations. The principal cannot evaluate the entire population and therefore delegates the task to the agency. Each potential regulation has a “trait,” which is the regulation’s suitability for achieving the goal of the principal.42

Bias presents a recurring concern in the analysis of administrative agencies. Agencies are often presumed to have interests that diverge from those of the principal. The agency may differ from the principal in its evaluation of potential regulations. Indeed, mitigating such conflicts is one of the central questions of administrative law and administrative law scholarship. This scholarship debates the efficacy of different mechanisms, such as cost-benefit analysis, judicial oversight, executive branch oversight, and public oversight (for example, the Freedom of Information Act), for reducing costs of errors.43 Each method brings pluses and minuses, but all of the methods leave agencies unbounded.44 No matter how strict the oversight, any proposed rule that survives the oversight process becomes a regulation. So long as the cost-benefit analysis proves that the regulation has positive net benefits, or the regulation follows the statute, or the regulation passes through appropriate executive or judicial oversight, the regulation may be issued. Because there is no hard ceiling or floor on regulations, agency regulations are promulgated in an unbounded institutional environment.

The regulatory environment need not be unbounded. The number—or more plausibly the value45—of regulations could be constrained by statute. The much-discussed concept of a “regulatory budget” imposes limitations on the costs that may be imposed by agencies via regulation. A recent Organization for Economic Cooperation and Development (OECD) report described a regulatory budget as follows:

The regulatory budget operates by close analogy to the traditional fiscal process. For example, each year (or at some longer interval), the government would establish an upper limit on the costs of its regulatory activities to the economy and would apportion this sum among the individual regulatory agencies. This would presumably involve a budget proposal developed by a regulatory oversight body in negotiation with regulatory agencies, approved by the executive branch of government, and submitted for legislative review, revision and passage. Once final budget appropriations were in force, each agency would be obliged to live within its regulatory budget for the time period in question.46

A regulatory budget provides the bounded institutional counterpart to the conventional unbounded regulatory environment.47 Although the concept of a regulatory budget is more than thirty years old, regulatory budgets are rarely implemented.48 This section analyzes when to choose regulatory budgeting versus conventional regulatory oversight as a method for reducing agency errors and bias.

The analysis in the previous two Parts offers several reasons to believe that bounded institutional structures such as regulatory budgeting may prove superior to traditional unbounded oversight methods. Bounded structures are particularly attractive when agent bias and error are more pervasive, when there are no accurate rules to restrict agent discretion, when the cost of agent errors is nonlinear, and when the sample population assessed by an agent is large. These features describe many regulatory environments. At the same time, other features of the regulatory environment, such as the principal’s probable ignorance of the population distribution of regulations and the difficulty of quantifying a regulatory budget, counsel against universal application of a bounded institutional structure. Instead of an all-or-nothing approach to regulatory budgeting, wherein a regulatory budget is either applied to all agencies or none, the analysis provided here suggests that a regulatory budget may be appropriate for some agencies but not others. Alternatively, it may be appropriate for the head of an agency to impose a regulatory budget on a sub-agency but inappropriate for Congress to impose one on an entire agency.

1. EPA Regulations: The Case for Bounded Institutions

To be concrete, consider a possible environmental regulation issued by the EPA. When promulgating environmental regulations, the EPA serves as an agent of Congress and the President under a variety of statutes, including the Clean Air Act. Many have accused the EPA of having a pro-environmental, anti-business bias. Oversight mechanisms, such as cost-benefit analysis, executive oversight via the Office of Information and Regulatory Affairs (OIRA), and judicial review, focus heavily on the EPA’s regulations. The EPA has authority to consider a wide range of regulations, from clean water standards49 to greenhouse gas emissions.50 In addition, crafting environmental regulations is hard to specify by rule. Indeed, many environmental statutes specify vague standards for the EPA to follow.51

Suppose that the EPA—pursuant to its authority under the Clean Air Act—is considering a set of regulations to remove air pollutants.52 Further suppose that the EPA is biased: it places a value on clean air that is double the value that Congress would place on clean air. In addition, Congress lacks the ability to specify by rule the regulations that it views as desirable. Finally, suppose that Congress has a sense of the amount of GDP it is willing to spend on clean air and specifies this number in a regulatory budget.53

Under these conditions, a regulatory budget outperforms conventional regulatory oversight mechanisms. The budget compels the EPA to regulate according to Congress’s preferred amount. But even if the EPA is constrained in the costs of regulations it can promulgate (“how much regulation”), how do we know that the agency will choose the right regulations (“which regulations”)? The EPA chooses the right regulations because it values clean air twice as much as Congress does. It will try to maximize the value of clean air, and achieving this objective requires the EPA to choose the regulations that provide the cleanest air possible subject to the budget constraint imposed by Congress. These are the same regulations that Congress would choose. Because Congress has specified its clean air “budget,” the fact that the EPA values clean air more than does Congress imposes no costs.54

Conventional oversight mechanisms, by contrast, fail to guarantee that the EPA’s bias in favor of clean air will produce the right regulations. Judicial oversight means that the EPA will choose the regulations that are easiest to justify under the relevant oversight standard. Choosing regulations in this manner leads to over-regulation because of the EPA’s bias. In addition, the EPA’s regulations may not produce the cleanest air per unit cost. Instead of seeking the most efficient regulations, the EPA seeks the regulations that are most likely to pass judicial muster.

A similar story applies to executive oversight. The EPA will attempt to implement its clean air bias by choosing regulations that appeal to its executive overseers at OIRA or other relevant centers of oversight within the White House. As with judicial oversight, these regulations will likely be greater in quantity and less efficient than the regulations that would be chosen under a regulatory budget.

Among the traditional unbounded oversight mechanisms, cost-benefit analysis (CBA) provides the closest analogue to a regulatory budget. CBA requires agencies to quantify the benefits and the costs of each regulation, and regulations are warranted if benefits exceed costs. Cost estimation is therefore required of both regulatory budgeting and cost-benefit analysis. CBA differs from regulatory budgeting in asking for quantification of regulatory benefits.

CBA’s quantification of benefits yields advantages and disadvantages. On the plus side, accurate calculation of costs and benefits produces optimal regulation. Congress wants regulations for which benefits exceed costs, and accurate CBA realizes this aim. The bounded structure of regulatory budgeting, by contrast, introduces rigidity that is costly if agents accurately estimate costs. An agency subject to a regulatory budget may forego positive value CBA projects or undertake negative value CBA projects.

CBA’s disadvantages arise when the agent has a biased view of the benefits of a regulation. In our hypothetical, cost-benefit analysis produces too much regulation because the EPA values clean air (the benefits of regulation) more than Congress does. Using CBA, the EPA will choose the right regulations—the ones that produce the cleanest air per dollar—but there will be too much regulation because the EPA values clean air more than Congress does. If OIRA or some other oversight body can “correct” the EPA’s overvaluation, then CBA can produce the right amount and types of regulations, but this requires the oversight body to monitor effectively the EPA’s estimates of both costs and benefits.

By bounding the cost of regulations, by contrast, regulatory budgeting does not demand that Congress or any other oversight body obtain good information about the value of clean air. So long as the EPA shares Congress’s rank ordering of benefits of clean air, and the costs of the EPA’s regulations are quantifiable, the bounded regulatory budget produces an efficient outcome—though, as indicated in the next section, this does not hold true when some assumptions are relaxed.

2. EPA Regulations: The Case Against Bounded Institutions

The previous section told a rosy story about the benefits of a bounded institution—regulatory budgeting—relative to the performance of more conventional unbounded institutions. The case for regulatory budgeting, however, rests on several assumptions that may be unrealistic. This section considers the efficacy of the bounded institution when these assumptions are relaxed.

a. Quantifiability

In order to impose a bound, Congress (the principal) must be able to quantify and measure the value of the bound. In the regulatory budgeting context, the bound is the cost imposed on the public by regulations issued by the agency. From an ex ante perspective, the cost imposed by regulation is very difficult to know with precision. Instead, the costs must be estimated. (Indeed, this prediction difficulty is one of the weaknesses of cost-benefit analysis.55) Regulatory budgeting requires that agency discretion be curtailed by a bound premised on an estimate. Other oversight mechanisms, such as judicial oversight, may be flawed—but they don’t rely on a false precision.

The critique is an important one. Regulatory budgeting is not like ordinary budgeting. If estimates of regulatory costs prove to be inaccurate or manipulable, then regulatory budgets do not yield the intended outcomes. If the EPA manipulates costs to appear lower than they actually are, then the EPA will produce too much clean air regulation. And if some types of regulation have costs that are easier to manipulate than others, then we may get the wrong regulations in addition to having too many.

But we should also not overstate the quantifiability problem for regulatory budgeting. CBA, which assumes a large role in the EPA regulatory process, requires the EPA to estimate both costs and benefits. Regulatory budgeting requires only costs to be estimated.56 And costs, which are often direct and pecuniary (such as the cost of pollution-reducing equipment for a power plant), are likely easier to estimate than benefits.57 If CBA can work, then so can regulatory budgeting.

b. Knowledge of the Distributional Parameters

A more problematic assumption that boosted the case for a regulatory budget at the EPA was the assumption that Congress knows the distribution of regulatory outcomes. This means that—although Congress cannot perfectly evaluate any particular regulation—it has a good sense of the “population parameters” of environmental regulations.58 A Congress that has a rough sense of the goals it wants to achieve through environmental regulation, but not a good sense of precisely how to achieve them, can reasonably choose the dollar value of regulations it wants, leaving the content of the particular regulations to the EPA. But if Congress does not have a sense of what is out there, then its bound will likely be flawed. And an EPA subject to a flawed bound may produce worse outcomes than an unbounded but biased EPA.

Legislators are not environmental rule-makers, and Congress is unlikely to have a good sense of the distribution of the effects of environmental regulations. This provides a strong argument against imposing a regulatory budget on the EPA.

But bounded institutions in the form of regulatory budgets may have benefits at other points in the regulatory oversight process. For example, OIRA, which is more sophisticated than Congress in evaluating environmental regulations, may be able to acquire a sense of the distribution of possible environmental regulations, even if it does not have the resources to examine every possible regulation. In addition, OIRA may have less of a pro-environment bias than the EPA.59 As a result, a regulatory budget formed by OIRA may have the advantages of a bounded institution without some of the disadvantages that accompany a regulatory budget formed by Congress. Indeed, learning the distribution of regulatory possibilities and then “getting out of the way” by imposing a regulatory budget may prove to be an easier task for OIRA than the task of overseeing all regulations and cost-benefit analyses.

And we should not be too quick to dismiss the possibility of a congressional regulatory budget for the EPA. Congress knows little about the distribution of environmental regulations, but it also knows little about budgeting requirements for different agencies—and still somehow passes an annual appropriations bill (or at least a continuing resolution). Regulatory budgeting may not be all that different from conventional bounded budgeting procedures.

For example, the EPA might submit an annual regulatory budget request to Congress each year. These submissions might give Congress the opportunity to learn more about the distribution of regulatory effects for environmental regulations. While Congress is unlikely to attain a comprehensive understanding of the population of existing and possible environmental regulations, it—or at least the relevant committee staffs—may be able to achieve a rough sense of the possibilities. If regulatory bias is a significant problem, then Congress may be better off with a regulatory budget based on imperfect distributional information than the unbounded regulatory systems currently in operation.

B. Mandatory Versus Discretionary Spending

We have already examined the problem of government spending on scientific research through the NSF. But the bounded versus unbounded divide also pervades government appropriations. Government spending takes two primary forms: discretionary and mandatory. Discretionary spending refers to “the budget authority provided by annual appropriations acts and the outlays that result from that budget authority.”60 Appropriations acts (or continuing resolutions extending previous appropriations acts) specify spending amounts for federal government activities. For example, the Consolidated Appropriations Act of 2012 specifies “[f]or compensation of the President, including an expense allowance at the rate of $50,000 per annum as authorized by 3 U.S.C. § 102, $450,000.”61

Mandatory spending means “budget authority and outlays provided by permanent laws.”62 Medicare, for example, is enacted by 42 U.S.C. § 1395 and does not require annual renewal. Instead, Medicare and Social Security are funded by federal trust funds that require mandatory transfers from designated revenue sources.63 Many mandatory spending programs, such as Social Security and Medicare, are commonly known as “entitlement” programs.

Entitlement spending programs constitute unbounded institutional structures. Congress is the principal, and the agency charged with administering the entitlement program (such as the Social Security Administration or the Centers for Medicare and Medicaid) is the agent. There is no restriction on how much or how little is spent on entitlement programs. Instead, the costs of entitlement programs are generally determined by eligibility requirements. For example, Medicare applies to all citizens and permanent residents aged sixty-five and older.64 In entitlement programs, the “to whom” question is specified by law, but the question of “how much” is unbounded. Indeed, the “how much” question is generally determined on an as-needed basis. If doctors and patients demand more medical spending for those over age sixty-five, then Medicare will cost more. The beginning of the Medicare Act, for example, states:

Nothing in this subchapter shall be construed to authorize any Federal officer or employee to exercise any supervision or control over the practice of medicine or the manner in which medical services are provided, or over the selection, tenure, or compensation of any officer or employee of any institution, agency, or person providing health services . . . .65

Discretionary spending programs, by contrast, are bounded institutional structures. Congress is the principal, and the department or agency receiving the appropriation is the agent. A department or program cannot spend more in a given year than its appropriation. According to the Consolidated Appropriations Act, the President’s salary is $450,000, no more or less.66 Once spending has been appropriated, the executive branch even has limited ability to spend less than the appropriated amount.67 The appropriation provides a bound to the cost of any programs. This bound contrasts with the explicitly unbounded nature of Medicare spending.

Most mandatory spending programs can be converted into discretionary spending programs. Medicare is an unbounded entitlement spending program, but it could be converted to a bounded discretionary spending program by appropriating a certain amount each year for each of its functions. This would require Medicare “rationing,” but rationing is commonplace in government spending. The administrator of the Medicare program, the Centers for Medicare and Medicaid Services (CMMS), was appropriated a certain amount, $3,879,476,000 in fiscal year 2012,68 and must “ration” this appropriation to carry out CMMS’s responsibilities as well as possible. So Medicare’s administrators are subject to rationing, even if the program they administer is not. Indeed, there are many proposals to convert unbounded entitlement spending programs into bounded programs. Proposals to convert Medicaid payments to states from sharing formulas to block grants of fixed dollar amounts seek to transform Medicaid from an unbounded spending program to a bounded spending program.69

Conversely, most discretionary spending programs can be converted into mandatory spending programs. Instead of appropriating money to departments and agencies on an annual basis as Congress does with bounded discretionary spending, Congress could pass laws funding such departments in perpetuity, on an as-needed basis. The President’s salary could be determined by an agency that sets salaries to be comparable to similar positions in other sectors. While as-needed funding may sound curious, recall that this is exactly the unbounded framework that characterizes entitlement programs such as Medicare and Social Security.70 Medicare pays for all eligible expenses, with no explicit rationing.

Scholars have offered surprisingly little analysis of the efficacy of mandatory versus discretionary spending programs.71 But the bounded versus unbounded institutional structure developed here provides a framework for understanding this issue. Mandatory spending rules work best in contexts that favor unbounded rules. Discretionary spending formulas function better when a bound cabins agent error effectively.

The largest entitlement spending programs often determine eligibility by rule according to a clearly defined metric. Medicare, for example, applies to permanent residents over age sixty-five.72 Social Security eligibility is determined by a statutorily defined rule that is a function of contributions to the program and age.73 Medicaid and Children’s Health Insurance Program (CHIP) eligibility are primarily functions of income, age, and family status—all quantifiable and verifiable metrics.74 The analysis above suggests that when rules regarding verifiable metrics are available, unbounded institutional structures tend to outperform bounded structures. Bounded institutional structures impose some rigidity but reduce bias. Because rules reduce the scope for bias, imposing a bounded structure when a rule is available—as in the case of Medicare, Social Security, and Medicaid—introduces rigidity with relatively little scope for bias reduction.

But the efficacy of rules is not constant across all entitlement programs. Rules function particularly well in the context of the Old-Age and Survivors (OAS) insurance component of the Social Security system.75 Because the Social Security benefit rule for retirees answers the questions of “to whom” and “how much,” imposing a bounded dollar amount on the program would introduce rigidity without diminishing any obvious sources of bias.76 For Medicare and Medicaid, rules provide a clear answer to the eligibility question (“to whom”), but no obvious answer to the question of “how much” the program should spend. At present, the amount is determined at the discretion of other agents, such as doctors and patients. These agents may well be biased.77 As a result, Medicare may be a candidate for a rule/bound combination, in which the rule determines eligibility and the bound determines how much can be spent. Indeed, the bound may be expressed in per capita terms—for example, a budget of $X per eligible participant—to minimize the rigidity imposed by the bound.78 With a hard budget in place for a fixed group of subjects, agents such as doctors and administrators would find biases constrained by the budget. Forced to keep spending within the bound, they may allocate more effectively in the partially bounded context than in the unbounded context that characterizes Medicare and Medicaid currently.

The disability insurance (“DI”) component of Social Security79 also creates tensions for the unbounded structure. For disability, the “how much” per person question is determined by rule. Once someone is found to be disabled, he or she receives benefits according to a formula based on past earnings.80 Determining disability (“to whom”), however, is not amenable to rule-delimited decision making because disability is a multi-dimensional and context-specific determination—what is disabling for one person or one job may not be disabling in another context. At present, disability determinations are made through a complex administrative process that must consider a wide variety of illnesses and definitions of disability.81 This process, which is controlled by administrators, may be prone to bias or systematic error. In addition, the population of individuals applying for DI is likely to be relatively constant or to change predictably from year to year. Under these conditions, bounds are well suited to cabining agent bias or error.

The bound on DI could be introduced in one of two related ways. First, Congress could place a bound on the number of disability recipients per year. If each administrator of the system were to receive a random sample of a large number of DI applicants, then the bound could be subdivided such that each administrator can make a bounded number of disability determinations. A “curve” for DI determinations would fulfill many of the criteria for an optimal bounded structure. DI determinations are made by agents who may be biased and error prone but likely share Congress’s general ranking of disability severity. In these circumstances, a fixed number of “yes” determinations per agent ameliorates bias and error; in addition, establishing a “curve” will not induce a great deal of incorrect DI decisions, because each administrator will see a large number of randomly drawn DI applicants, and the distribution of disability in the population is likely to be constant or to predictably change from year to year. Second, a bounded dollar budget could be placed on the disability insurance system. In this case, a primacy rule would be used to decide what to do when the bounded budget conflicts with the benefits mandated by rule.

Discretionary spending programs often display the characteristics of programs that would benefit from bounds. Consider the budgets of most cabinet departments and administrations. Unlike income support programs such as Social Security, it is difficult to specify budgets via rule; the decision regarding how much should be spent is too multidimensional. Delegating budgeting decisions to agents in an unbounded way may lead to considerable bias. A mandatory program calling for agencies to receive whatever budget they request would likely lead to too much spending. The agency will often have a more generous view of its spending needs than Congress does. Just as the EPA, for example, may issue regulations that exceed Congress’s ideal level, so too might the EPA request a greater appropriation than Congress deems warranted, because a higher appropriation enables the EPA to protect the environment more effectively. In addition, the annual nature of the appropriations process gives Congress an opportunity to get a sense of the distribution of needs in different agencies and how likely these needs are to vary. This learning process allows Congress to set reasonable bounds. In total, many programs subject to discretionary spending allocations have attributes that make them conducive to bounded institutional structures.

While the bounded institutional structure of many discretionary spending programs is appropriate, there are other currently bounded programs that—based on the analysis above—should probably be unbounded. Consider FEMA spending. Disasters, and especially large disasters, are rare events. Their number and cost may change dramatically from year to year. With such a variable distribution, a bounded institutional structure can produce bad outcomes. If the budget is fixed but there is a much higher than expected number of disasters, then disaster victims may receive much less than Congress would like. If there are fewer disasters and FEMA has a fixed budget, then disaster victims may receive too much. Both possibilities are costly and will occur frequently if FEMA has a fixed budget to provide for disaster relief. A mandatory spending program that dictates that disaster victims should receive what FEMA thinks appropriate, though prone to bias, would avoid the bad outcomes of over-allocation if there are few disasters or under-allocation if there are many disasters. Of course, Congress can augment a discretionary annual appropriation with an emergency appropriation in the event of higher than expected disaster costs. This effectively replaces a bounded discretionary spending allocation with an unbounded allocation. But passing supplementary bills imposes costs. Congress may not be able to pass bills expeditiously, as demonstrated by the recent brouhaha concerning a relief bill for the costs of Hurricane Sandy.82 Congress is also unlikely to pass a bill reducing FEMA spending if there are fewer disasters than expected.83

Some types of defense spending also appear ill-suited to bounded spending restrictions. While some aspects of defense spending have predictable distributions from year to year (for example, regular personnel costs, long-term procurement programs), other aspects of military spending are less predictable. Wars are expensive, and we cannot rely on the law of large numbers to guarantee that the expenses average out. Exclusive reliance on bounded defense spending would produce too much spending in peaceful years and too little in times of war. As a practical matter, our budget process recognizes this mismatch. While much of defense spending is bounded and “discretionary,” additional expenditures required for war are often the subject of supplementary budget proceedings.84 But, as with FEMA spending, these supplementary proceedings are simply another way to make a bounded program less bounded. Passing additional war-related spending bills imposes transaction costs, and it is unlikely that times with less than the average number of wars will lead to a reduction in military expenditures. Both of these considerations weigh in favor of an unbounded spending program for war-related costs.

The fact that wartime spending does not fit all the criteria for an ideal discretionary program does not mean that an unbounded program is superior. War-related decisions may be subject to considerable bias from agents, and a bound would mitigate this bias. In addition, war-related decisions are difficult to specify via rule. As a result, the hybrid system currently in use, with bounded defense discretionary spending and periodic war-related supplementary budgets, may do the best job of containing bias (by requiring legislative debate) while encouraging the flexibility needed to handle uncertain war expenses.

C. Minority Set-Asides and Croson

The bounded versus unbounded framework applies to the question of minority set-asides discussed by the Supreme Court in Fullilove v. Klutznick85 and City of Richmond v. J.A. Croson Co.86 Minority set-asides seek to remedy past and current discrimination by requiring minimum percentages of the value of government contracts to be used to hire minority business enterprises. In Croson, for instance, the City of Richmond, with a 50% African-American population, “required prime contractors to whom the city awarded construction contracts to subcontract at least 30% of the dollar amount of the contract to one or more Minority Business Enterprises” (MBEs).87

The Croson policy and similar policies adopted by other states are bounded institutional structures. The principal—the City of Richmond—sought to ameliorate past and present discrimination.88 Therefore, it bounded the choices of its agents—the prime contractors. Concerned about bias by the prime contractors toward some subjects (MBE subcontractors), Richmond required that 30% of subcontracts be granted to MBEs.89

The City of Richmond could have chosen an unbounded structure to compensate for possible agent bias. For example, Richmond could have insisted that prime contractors give MBEs a “close look.” With this unbounded policy, Richmond could have stated its policy preferences but given the agents discretion in fulfilling the city’s preferences. On the other hand, Richmond could have said that any bid by MBEs that was within 5% of the lowest non-MBE bid must be accepted. This alternative would have imposed a rule relating to subcontracting with minorities but would not have bounded the dollar value of subcontracts with MBEs.

As detailed in the previous sections, Richmond’s choice of minority set-asides—a bounded structure—offered advantages and disadvantages. If the City of Richmond cannot judge subcontractor bids but has a good sense of how many MBEs it wants to hire, then the minority set-aside can produce an ideal outcome. The prime contractors would choose the best MBEs using their superior judgment of quality, but the prime contractors’ racially biased preferences relative to the city would be offset by the set-aside requiring that 30% of value be granted to MBE subcontractors.

In other circumstances, the set-aside policy would produce inefficiencies relative to unbounded alternatives. If prime contractors are not particularly biased against MBEs, then the set-aside introduces rigidity without much benefit. If Richmond does not have a realistic sense of its preference for MBE subcontractors, then the set-aside could produce very inefficient results, with too many expensive or ill-qualified MBEs. If the quality of MBEs varies widely, or if there are only one or two subcontracts per contractor, then there is a much greater chance that the set-aside will result in more MBEs than the city would want if it had perfect knowledge of subcontractor quality and race.

This rigidity was criticized by the Supreme Court in finding Richmond’s policy unconstitutional under the Fourteenth Amendment:

The Richmond Plan denies certain citizens the opportunity to compete for a fixed percentage of public contracts based solely upon their race. To whatever racial group these citizens belong, their “personal rights” to be treated with equal dignity and respect are implicated by a rigid rule erecting race as the sole criterion in an aspect of public decisionmaking.90

There is no doubt that, as described, the bounded set-aside creates a “rigid rule.” But the analysis of this Essay demonstrates that, under the right conditions, the Supreme Court’s critique of Richmond’s policy is inapt. Indeed, a bounded set-aside can produce an ideal outcome that would not be feasible with a seemingly less rigid rule.

When there are many MBE and non-MBE subcontractors, a set-aside becomes one factor among many that determines who receives subcontracts. For example, a bounded rule, such as a set-aside, does not “erect[] race as the sole criterion . . . of public decisionmaking.”91 The set-aside ensures that race is accounted for, but the use of bounded criteria allows for consideration of an infinite number of dimensions of “quality.” Instead of requiring subcontractors to comply with a formula for how to weigh MBE status against other dimensions of quality such as price and expertise, the set-aside allows each contractor to make decisions based on the criteria that he or she thinks are most important—while ensuring that the interest in ameliorating discrimination is realized. In addition, the bound may treat people with “equal dignity”92: if the size of the set-aside quota accurately reflects Richmond’s legitimate interests in ameliorating past discrimination, then the set-aside allows contractors to make subtle and individualized decisions in choosing among MBEs and non-MBEs.

In Croson, there was only one MBE. In these circumstances, bounded institutions such as set-asides perform poorly. Set-asides introduce rigidity, such as (in Croson) requiring the only marginally qualified MBE to be chosen as a subcontractor. Such rigidity might appear to preclude equal dignity and respect in decision making. But this does not mean that set-asides are generally a bad idea. In cases where (1) current or past racial bias is prevalent, (2) there are many MBE and non-MBE subcontractors, (3) there is no viable rule dictating the weight to be placed on race relative to other factors, and (4) the principal cannot judge the quality of subcontractors, then, as shown in Part II, set-asides can produce excellent outcomes.

To sum up, analyzing Croson in light of our study of bounded versus unbounded institutions suggests that the problem is not racial set-asides per se, but rather the use of set-asides in appropriate circumstances.

D. Judicial and Quasi-Judicial Decision Making

In many contexts, society charges an agent with making a series of decisions about subjects. The agent’s decision-making process is often unbounded—even though the agent may well be biased in a socially undesirable manner. The determination of disability benefits described above is one such circumstance. Society has some sense of who should receive disability benefits and who should not. If an administrative law judge systematically awards benefits to more or fewer applicants than society would prefer, then there is a social cost. Bounded institutional structures can mitigate the costs of agent bias.

Bounded institutional structures work best when the distribution of the subject population presented to the agent is relatively constant and large, the agent’s decisions are quantifiable, and the agent shares a rank ordering of subjects with the principal. These conditions may be met in many judicial and quasi-judicial decision-making processes. Consider criminal sentencing. A judge makes sentencing decisions for a large number of offenders who are randomly assigned to the judge. Some judges impose harsher sentences, while others are more lenient. Society demonstrates great concern about the possible biases of these judges.93 Indeed, the Federal Sentencing Guidelines attempt to reduce the scope of judicial discretion in sentencing94 by imposing intricate sentencing rules. The Guidelines continue to generate considerable controversy.95

A bounded sentencing structure offers an alternative means of constraining judicial bias without intruding into the judicial decision-making process. Each judge in a district96 could be given a “sentencing budget” that is determined by Congress.97 The budget could be specified for each offense type98 or for all offenses put together and, if necessary, could span several years to minimize the problem of random variations in subject population. With a sentencing budget and random assignment of offenders to judges, each judge should have a relatively similar population of offenders, particularly if the time frame is long enough to allow natural variation to balance out. Under these conditions, a bounded structure (a sentencing budget) reduces bias with little cost in rigidity so long as the judge shares a rank ordering of offense severity with society.99 In effect, society says, “We expect you to have to give out x years of sentences; you decide how to do it.” The “x years” criterion ensures that neither harsh judges nor lenient judges are able to impose their biased views upon the offenders who happen to come before them. If the judges share society’s rank ordering of “to whom,” then a sentencing budget mitigates or even eliminates bias without the intrusiveness of an intricate rule-based system, such as the sentencing guidelines.

Bounded institutional structures are also promising in the context of judging immigration asylum cases. Congress wants some—but not all—foreigners residing in the United States to enjoy asylum (that is, those facing certain dangers in their home countries). Congress’s perception of the desirability of asylum likely depends on many hard-to-define factors, such as the presence of reasonable fear of harm or the denial of important rights in the asylum seeker’s home country. Congress vests the power to grant asylum to both U.S. Citizenship and Immigration Services (USCIS) in the Department of Homeland Security (DHS) and the Executive Office for Immigration Review (EOIR) in the Department of Justice.100 These offices further specify standards and make decisions, and asylum officers and immigration judges apply these standards.101 This delegation policy introduces many problems. With such ambiguous standards, agents have the ability to indulge biases for or against asylum,102 to opine on issues on which the agents have little experience, or to adopt whimsical notions of how to apply the standards.103

A bound on each judge who grants asylum would likely produce better outcomes. For example, Congress could specify that a bounded number of people should receive asylum from each immigration judge each year (or provide a bound to asylums from an immigration judge over a multi-year period in order to raise the number of immigration applicants that each immigration judge sees when applying the bound). The bound on asylum numbers should mitigate immigration judges’ biases and restrict judges’ ability to apply whimsical criteria. Biases will be directly reduced by the bound. If a particular immigration judge is systematically biased against asylum seekers relative to Congress, then Congress’s bound will force the judge to grant more asylums than she otherwise would. If another immigration judge is biased in favor of asylum, then the specified bound will restrict the number of applicants to whom the judge can grant asylum. The bound may also discourage immigration judges from indulging whimsical notions of eligibility. If the whimsical notion keeps a deserving applicant out, it also means that a less deserving applicant gets in. And so a biased immigration judge will be less likely to indulge her biases in an idiosyncratic way because the idiosyncrasy does not facilitate the bias—for example, fewer asylum recipients—but rather allocates the benefit in a way the judge does not want—for example, she grants asylum to less deserving applicants.

This is not to say that a bound works perfectly. The number of people whom Congress would deem worthy of asylum may fluctuate unpredictably from year to year, and setting a precise number of asylum recipients does not allow the agents to adjust to the fluctuation. If Congress could express its asylum preferences perfectly via an enforceable rule, then the rule would be preferable, since it would ensure that the right applicants receive asylum without imposing a constraint on the number. But a rule is almost certainly infeasible in this case. And so Congress should weigh the bias reduction and thought clarification benefits of a bound (combined with a standard) against the cost of the rigidity the bound imposes. Congress may well decide that the benefits of the bound combined with the standard exceed the costs.

Indeed, bounded institutional structures can ameliorate agent bias in almost every context in which agent bias is a problem. We can imagine “stop, question, and frisk” budgets assigned to the police to bound their ability to engage in aggressive forms of policing; “summary judgment budgets” to standardize the difficult-to-police burden of “summary judgment”; “tort budgets” to reign in judges or districts that are perceived as too plaintiff-friendly or defendant-friendly; “discrimination budgets” to address disparities in judges’ propensities to allow employment discrimination suits; sentencing budgets for prosecuting attorneys’ offices to mitigate the problem of prosecutorial over-reach or under-reach; and patent budgets to ensure that the Patent and Trademark Office or individual patent examiners do not award patents to innovations that are insufficiently novel (or fail to grant patents to original products).104

In all of these cases, and many others that have not been identified, the bounded institutional structure—some form of hard budget constraint—offers bias reduction at the cost of rigidity. Whether this trade-off is justified depends on the institutional setting. When more factors favoring bounds are present, the setting is more conducive to the use of budgets.

One particularly important factor in all of these contexts is the quantifiability and non-manipulability of the item subject to the budget. For example, if “stop, question, and frisk” is ambiguously defined, then the ability to bound the agent’s behavior is limited.105 Agents can manipulate the ambiguity in the definition to avoid the bias-ameliorating features of the bounded constraint. Thus, the ability to quantify—and the difficulty of manipulating—the bounded constraint is worth reemphasizing.

E. Timing

When grading, a professor sees the quality of the entire group of students at one time. In the examples mentioned above, the agent evaluates the subjects over time.106 This may lead to some complications. For example, early within a sentencing budget period, a judge or prosecutor may be excessively cautious, preserving too much of the budget for egregious future criminals who never appear.107 Alternatively, a judge may find that she has allocated too much of her sentencing budget to her early offenders, meaning that there is little left in the “budget” for heinous offenders.

Several considerations suggest that though the timing problem is real, it should not necessarily prevent policymakers from imposing bounded institutional constraints. First, any budget has a timing problem. When Congress allocates money for a purpose, the recipients of the money must ensure that the funds last the full year. With practice and careful observation, agents can be taught to use the budget appropriately.108 Second, there may be ways to adjust the treatment of the early arrivals ex post to ensure equal treatment with late arrivals. For example, if a judge finds that she has been too strict with her early offenders, she can be allowed to cut some of the sentences she has already meted out to ensure an adequate budget for the remainder of the period.

Third, and most importantly, the potential costs of the timing problem for bounded constraints can be mitigated by using bounded intervals rather than exact numerical bounds. Judges, for example, can be given a sentencing budget interval rather than a precise sentencing number. In our example from the previous section, the judge may be granted a sentencing budget of between thirty-five and forty-five months rather than a hard bound of forty months. The interval allows for some slack in the budget, mitigating the harm caused by over- or under-aggressive use of the budget on early arrivals relative to late arrivals. Of course, the interval also partially undermines the purpose of the bounded constraint, because the interval allows some scope for biases to be realized. Nevertheless, a bounded interval combines some of the benefits of bounded constraints—preventing the realization of systematic bias that is greater than the size of the interval—while mitigating some of the bounded constraint’s most significant costs.

Conclusion

Bounded institutional structures provide legislatures with a useful tool for delegating authority to agents, such as administrative agencies or courts. This Essay has established circumstances under which bounds are most effective—when (1) agents are likely to be biased, (2) rules that constrain agent biases are impractical, (3) quality variation between subjects is limited, and (4) the number of subjects evaluated by each agent is large.

In addition to this analysis of the optimal use of bounds, the Essay has a broader normative and methodological goal. While legislative delegation to agencies and courts is an exhaustively studied topic,109 scholarly writings suffer from insufficient attention to the economic literature on optimal delegation. The value of bounds (analyzed in a small and recent offshoot of this broader literature) is just one example of the many fruitful applications of the optimal delegation literature.

Bounds should be used more often. Under certain conditions—conditions that are not inevitable but also not implausible—bounds offer a compelling solution to the problem of legislative delegation to agents. Bounds can allow legislatures to take advantage of an agent’s expertise without allowing the agent to indulge biases. Bounds therefore ameliorate the tradeoff between expertise and bias that forms the core of many problems of institutional design.110 Additional scholarly attention to bounds may result in the identification of more situations in which this solution to the Gordian knot of institutional design is relevant.

Please see the PDF for the technical appendix to this Essay.